ทฤษฎีควอนตัมมาจากไหน
สำรวจสามปริศนาทางฟิสิกส์ที่นำมนุษยชาติจากโลกคลาสสิกสู่ยุคของกลศาสตร์ควอนตัม
เผยแพร่เมื่อ:กลศาสตร์ควอนตัมถือเป็นหนึ่งในการปฏิวัติทางความคิดที่ยิ่งใหญ่ที่สุดในประวัติศาสตร์ของฟิสิกส์ แต่แนวคิดใหม่นี้ไม่ได้เกิดขึ้นอย่างโดดเดี่ยวหรือฉับพลัน หากแต่รายล้อมไปด้วยปัญหาทางฟิสิกส์ที่หลากหลายและความพยายามค้นหาคำตอบของผู้คนในหลายหลายยุค หากย้อนกลับไปช่วงปลายศตวรรษที่ 19 หรือรัชสมัยของรัชกาลที่ 4 และรัชกาลที่ 5 ฟิสิกส์คลาสสิกซึ่งเคยอธิบายการเคลื่อนที่ แรง และปรากฏการณ์ทางไฟฟ้าได้อย่างงดงาม เริ่มเผชิญกับข้อจำกัดจากการทดลองบางชุดที่ให้ผลลัพธ์เกินขอบเขตของคำอธิบายแบบเดิม
จากรากฐานแห่งความขัดแย้งนี้ และสับสนอนลหม่านนี้ นักวิทยาศาสตร์เริ่มตั้งคำถามต่อความเข้าใจเดิมเกี่ยวกับธรรมชาติของสสารและพลังงาน จนนำไปสู่การถือกำเนิดของทฤษฎีใหม่ที่เปลี่ยนวิธีที่เรามองโลกอย่างสิ้นเชิง นั่นคือทฤษฎีควอนตัมในยุคเริ่มแรกและต่อมาก็เป็นกลศาสตร์ควอนตัมที่ไฮเซนเบิร์กเสนอในปี 1925
ในตอนนี้ ขวัญตาจะพาไปสำรวจ “สามปัญหาสำคัญ” ที่เป็นจุดเปลี่ยนของประวัติศาสตร์วิทยาศาสตร์ และเปิดประตูสู่โลกวอนตัมที่ยังคงท้าทายความเข้าใจของมนุษย์จนถึงปัจจุบัน
ปัญหาแรก: การแผ่รังสีของวัตถุร้อน
ในช่วงปลายศตวรรษที่ 19 ไฟฟ้าเริ่มเข้าถึงผู้คนมากขึ้น พวกคนที่มีไฟฟ้าใช้ ส่วนหนึ่งก็มักจะมีวัตถุส่องสว่างที่เรียกว่าหลอดไฟด้วย ในยุคนั้นเทคโนโลยียังไม่ได้วิริศมาหราเท่ากับยุคปัจจุบัน หลอดไฟของพวกเขาทำงานอย่างง่าย ๆ เมื่อไฟฟ้าวิ่งผ่านขดลวดที่มีความต้านทานไฟฟ้าสูง ๆ มันก็ร้อนและเปล่งแสงออกมา พวกนักวิทยศาสตร์และอุตสหกรรมในขณะในรับรู้ถึงกฎที่เป็นธรรมชาตินี้อยู่แล้วว่า วัตถุที่ร้อนจะแผ่คลื่นแม่เหล็กไฟฟ้าออกมา ถ้ามันร้อนพอก็จะเปล่งแสงออกมาด้วยความยาวคลื่นที่ตาเรามองเห็น และยิ่งวัตถุร้อนขึ้นมากเท่าไหร่ก็จะเปล่งแสงออกมาที่ความยาวคลื่นสั้นลง
 ภาพหลอดไส้ที่ส่องสว่าง ภาพจาก Levi Frey
ภาพหลอดไส้ที่ส่องสว่าง ภาพจาก Levi Frey
แต่หากว่าคนในยุคนั้นมีเพียงคำบรรยายปรากฎการณ์นี้เท่านั้น ยังไม่มีใครที่มีคำอธิบายที่ดีเกี่ยวกับสาเหตุของปรากฎการณ์นี้ อย่างดีที่สุดในช่วงเวลานั้น นักฟิสิกส์ก็มีเพียงกฎของวีน (Wein’s law) ที่ประมาณค่าความยาวคลื่นที่วัตถุร้อนเปล่งออกมาและเข้มที่สุดในแต่ละอุณหภูมิ1 แต่ก็ไม่มีใครอธิบายว่าเหตุใดพวกมันจึงประพฤติตัวเช่นนี้ ซ้ำร้ายไปยิ่งกว่านั้น ฟิสิกส์ในยุคนั้นอย่างเรย์ลีและจีนส์ก็ได้ใช้ทฤษฎีที่มีอยู่ในตอนนั้น (ซึ่งภายหลังถูกเรียกว่าเป็นทฤษฎียุคคลาสสิก) ทำนายค่าความเข้มของแสงที่ความยาวคลื่นต่าง ๆ ที่วัตถุร้อนแผ่ออกมา เค้าพบว่าหากกฎทางฟิสิกส์ที่พวกเค้ามีนั้นถูกต้อง แสงที่ความยาวคลื่นต่ำ ๆ ก็ควรจะมีความเข้มเป็นอนันต์ ซึ่งฟังดูแล้วหันมามองโลกแห่งความเป็นจริง ที่ว่ามานั้นมันเป็นไปไม่ได้เลย เพราะหากเป็นเช่นนั้นจริง วัตถุที่ร้อนนิดหน่อยก็จะปล่อยแสงความยาวคลื่นต่ำเช่นรังสีแกมมา รังสีเอ็กซ์ออกมาเต็มไปหมดจนไปทำลายทุกสสารที่มีความสลับซับซ้อน ไม่เหลือสารที่จะมีโครงสร้างพอที่จะประกอบเป็นชีวิตขึ้นมาได้เลย
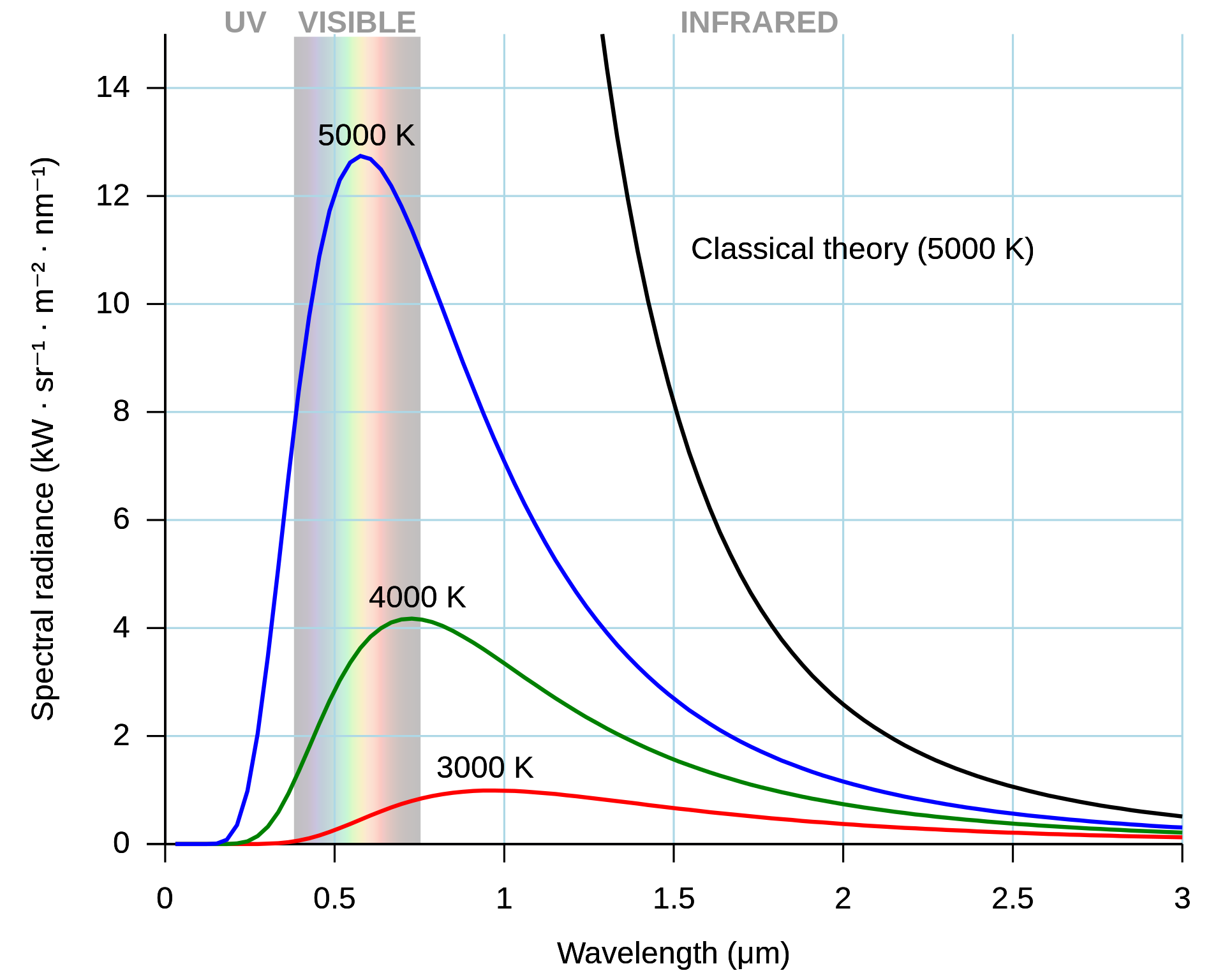 กราฟการแผ่รังสีของวัตถุดำที่อุณหภูมิต่าง ๆ ตามสมการของพลังค์ เปรียบเทียบกับการทำนายตามทฤษฎีคลาสสิกของเรย์ลี–จีนส์ ภาพจาก Darth Kule บน Wikimedia
กราฟการแผ่รังสีของวัตถุดำที่อุณหภูมิต่าง ๆ ตามสมการของพลังค์ เปรียบเทียบกับการทำนายตามทฤษฎีคลาสสิกของเรย์ลี–จีนส์ ภาพจาก Darth Kule บน Wikimedia
ทางออก
ในปี 1900 มักซ์ พลังค์ได้เสนอว่าวัตถุร้อนเหล่านี้ปล่อยพลังงานออกมาทางคลื่นแม่เหล็กไฟฟ้าในลักษณะที่เป็นก้อน ๆ (Energieelement)2 มีลักษณะเหมือนกับว่าเป็นเหรียญพลังงานแทนที่จะเป็นค่าเท่าใดก็ได้ (นึกถึงว่าเราใช้เหรียญได้เล็กที่สุดก็คือเหรียญ 25 สตางค์ ในขณะที่ถ้าเราโอนเงินเราจะโอนเศษสตางค์เท่าใดก็ได้) และค่าที่มันสามารถถ่ายโอนกันได้ก็แปรผันตรงกับค่าความถี่ ซึ่งแปลว่ามันผกผันกับค่าความยาวคลื่น ในสมการคณิตศาสตร์เขียนได้ว่า
เมื่อ E คือหน่วยที่เล็กที่สุดของพลังงานที่โอนถ่ายกันได้ คือค่าคงที่การแปรผัน คือค่าความเร็วของคลื่นแม่เหล็กไฟฟ้า ค่าความถี่ของคลื่นแม่เหล็กไฟฟ้าและ คือความยาวคลื่น
นี่เป็นจุดเริ่มต้นของการเปลี่ยนความเชื่อพื้นฐานของฟิสิกส์ที่ว่าพลังงานและปริมาณต่าง ๆ สามารถที่เป็นค่าอะไรก็ได้และมีความต่อเนื่อง จุดเปลี่ยนนี้แม้จะแปลก ๆ ดูไม่มีที่มาที่ไป แต่ก็ไม่ได้ฟังดูหลุดโลกอะไร แถมยังทำให้ผลลัพธ์ที่ตามมาตรงเผงกับค่าที่ได้จากการทดลอง โดยเฉพาะค่าความยาวคลื่นต่ำ ๆ ที่ผลการคำนวณพบว่ามันไม่ได้ปล่อยพลังงานออกมาเป็นอนันต์อีกต่อไปแล้ว
ปัญหาที่ 2: แสงเป็นอนุภาคหรือคลื่น และปรากฎการณ์โฟโตอิเล็กทริกซ์
แสงคืออะไร นี่เป็นคำถามที่นักวิทยาศาสตร์และนักปรัชญาต่างพยายามที่จะหาคำตอบและเสนอคำอธิบาย ความพยายามนี้มีมาตั้งแต่ที่เสนอว่าแสงนั้นเป็นรูปหนึ่งของธาตุไฟ (ของทางกรีกและโรมันโบราณ) ในยุคเรเนซองค์ เดการต์ได้เสนอว่าแสงนั้นเคลื่อนที่แบบฉับพลันทันใดและยังประพฤติตัวคล้ายกับคลื่น อันจะเห็นได้จากการหักเหของแสงเมื่อผ่านตัวกลางต่างชนิดกัน 3 แต่แล้วไม่นาน นิวตันก็ได้สนับสนุนทฤษฎีอีกทางหนึ่งที่ว่าแสงเป็นอนุภาค ผ่านจดหมายที่เขาส่งให้ราชสมาคมอังกฤษตีพิมพ์ในปี 1671 4 นอกจากนั้นเขาก็ปฏิเสธแนวคิดที่ว่าแสงเป็นคลื่น สาเหตุก็เนื่องจากว่าคลื่นจะต้องมีการเลี้ยวเบนเมื่อผ่านวัตถุที่มากำบังมัน ส่วนเรื่องการหักเหของแสงเขาก็อธิบายว่าเกิดจากความหนาแน่นที่มากกว่าทำให้อนุถาคของแสงถูกดูดให้เคลื่อนที่เร็วขึ้น (ดูหน้า 270-2 ในหนังสือ Opticks 5) ทฤษฏีของแสงของนิวตันนี้ได้รับความนิยมเทียบเคียงคู่กับทฤษฏีคลื่นของแสง เนื่องจากการทดลองที่ทั้งนิวตันและคนอื่น ๆ ทำเพื่ออธิบายทฤษฎีนี้ ความน่าเชื่อถือ และตำแหน่งแห่งที่ของนิวตัน6 จนกระทั่งวันหนึ่งในฤดูใบไม้ร่วงปี 1865 ที่สหราชอาณาจักร
 การหักเหของแสง ภาพจาก Rainald62 บนวิกิมีเดีย
การหักเหของแสง ภาพจาก Rainald62 บนวิกิมีเดีย
ในปี 1865 ชายวัย 34 ปีที่ชื่อ เจมส์ เคลิร์ก แมกซ์แวล์ (James Clerk Maxwell) เพิ่งเสนอทฤษฎีคลื่นแม่เหล็กไฟฟ้า7 ทฤษฎีนี้เป็นที่น่าสนใจของนักฟิสิกส์และนักประดิษฐ์ในยุคนั้นเป็นอย่างมาก หนึ่งในเหตุผลนั้นก็เพราะว่า เขามาร่วมตอบปัญหาว่าแสงนั้นคืออะไร และทฤษฎีของเขาก็ใช้ได้ดีจนกว่าที่ใคร ๆ จะปฏิเสธมันได้ ในทฤษฎีนี้แสงถูกจัดให้เป็นช่วงความถี่หนึ่งในสเปกตรัมของคลื่นแม่เหล็กไฟฟ้า หรือจะพูดให้สั้น ๆ ว่าทฤษฎีนี้บอกว่าแสงเป็นคลื่น อีกหนึ่งเหตุผลก็คือทฤษฎีนี้อธิบายความสัมพันธ์ระหว่างสนามไฟฟ้าและสนามแม่เหล็กไว้ว่าเป็นเสมือนกับเหรียญที่อยู่คนละด้าน สำหรับนักฟิสิกส์ทดลองแล้ว นั่นหมายความว่าเราก็ควรจะตรวจจับหรือว่าผลิตคลื่นแม่เหล็กไฟฟ้าด้วยอุปกรณ์ทางไฟฟ้าสักอย่างได้
ในสิบปีให้หลัง ปี 1886 ไฮน์ริช แฮทซ์ (Heinrich Hertz) ได้เสนอชุดอุปกรณ์ที่สามารถตรวจจับคลื่นแม่เหล็กไฟฟ้าได้ผ่านการสังเกตฟ้าแลปที่อยู่ระหว่างช่องว่างระหว่างขั้วไฟฟ้าสองขั้ว และก็ค้นพบด้วยกว่าหากฉายแสงที่ความถี่สูง ๆ (นั่นคือ ความยาวคลื่นต่ำ ๆ ) บนขั้วไฟฟ้าทำให้เจ้าสายฟ้าแลปนี้เกิดขึ้นได้ในช่องว่างระหว่างกันที่มากขึ้น8
จากนั้นในปี 1897 โยเซฟ จอห์น ทอมสัน (Joseph John Thomson) ก็แสดงให้เห็นว่าสายฟ้าที่แลประหว่างช่องว่างของขั้วไฟฟ้านี้เป็นอนุภาคชนิดเดียวกันกับรังสีที่เรียกว่ารังสีแคโทด9 กล่าวคือ ฟ้าแลปในอุปกรณ์ของแฮทซ์นั้นเกิดจากอิเล็กตรอนที่รับพลังงานคลื่นแม่เหล็กไฟฟ้าและหลุดออกมาจากตัวโลหะ แต่คำอธิบายนี้ก็ทำให้เกิดปัญหาตามมา เพราะถ้าเป็นเช่นนั้นจริง หากมีความเข้มแสงเพียงพอ ค่าความยาวคลื่นที่สูงกว่าก็ควรจะทำให้อิเล็กตรอนหลุดออกมาได้เช่นกัน เหตุที่ควรเป็นเช่นนี้ก็เพราะว่าพลังงานของคลื่นขึ้นอยู่กับทั้งความยาวคลื่นและก็แอมพลิจูดของคลื่น (ซึ่งคือความเข้มของแสงในกรณีนี้)
หลังจากนั้นไม่นาน ฟิลิปป์ เลอนาร์ด (Philipp Lenard) ก็แสดงให้เห็นผ่านการทดลองว่าความเข้มแสงไม่มีผลใด ๆ กับการทำให้อิเล็กตรอนหลุดออกมา และไม่มีผลต่อพลังงานของอิเล็กตรอนแต่ละตัวที่หลุดออกมาด้วย แต่สิ่งที่มีผลต่อพลังงานของอิเล็กตรอนก็คือความยาวคลื่นของแสงที่ใช้สาดไปที่โลหะ หมายความว่าเราต้องใช้ความยาวคลื่นที่สั้นพอหากจะอยากให้อิเล็กตรอนหลุดออกมา10 (11 page 26) ปัญหานี้ป็นที่น่าฉนงและได้รับการตั้งชื่อว่าเป็น “ปริทรรศน์ความสว่าง” (apparent paradox)
ต่อมาในปี 1905 ไอน์สไตน์จึงได้เสนอว่าอิเล็กตรอนน่าจะรับพลังงานจากคลื่นแม่เหล็กไฟฟ้าเป็นเฉพาะค่าบางค่าซึ่งเป็นค่าหน่วยพลังงานเดียวกันกับที่พลังค์เสนอ หรืออีกนัยหนึ่งแสงเมื่อถูกดูดกลืนพลังงาน พวกมันทำตัวเหมือนกับว่าแสงเป็นอนุภาคที่มีพลังงานเข้าไปชนกับอิเล็กตรอนและถูกดูดกลืนพลังงาน 12
แนวคิดนี้ยังนำไปสู่การทำนายพลังงานจลน์ของอิเล็กตรอนที่ถูกปลดปล่อยออกมาด้วยความสัมพันธ์ผกผันเชิงเส้นกับความถี่ของคลื่น ซึ่งต่อมาได้ถูกยืนยันด้วยการทดลองของโรเบิร์ต มิลลิแกน13 ผู้ซึ่งเป็นที่รู้จักจากการหาค่าประจุของอิเล็กตรอนด้วยการทดลองหยดน้ำมัน
ภาพแผนผังกระบวนการ photoelectric จาก Ponor บนวิกิมีเดีย
ปัญหาที่ 3: อิเล็กตรอนในอะตอม
ในปี 1911 แบบจำลองรัทเทอร์ฟอร์ดเสนอว่าอะตอมมีประจุบวกหนาแน่นอยู่ตรงกลางของอะตอมและมีอิเล็กตรอนพร้อมกับที่ว่างล้อมอยู่รอบ ๆ อย่างไรก็ดีอิเล็กตรอนเหล่านั้นไม่ได้ถูกอธิบายอย่างแน่ชัดว่ามันมีโครงสร้างได้อย่างไร ในเมื่อหากอิเล็กตรอนมันโคจรรอบอะตอมจริง ๆ อิเล็กตรอนเหล่านั้นก็ควรจะแผ่คลื่นแม่เหล็กไฟฟ้าออกมาตลอดเวลาจนอิเล็กตรอนมันหมดพลังงานและจมไปรวมกับนิวเคลียสตรงกลาง
อีกประเด็นที่เกี่ยวกับอิเล็กตรอนก็คือ เมื่อเราเอาสารจำพวกธาตุไปทำให้ร้อน เราจะเห็นว่าบางสารจะเปล่งแสงที่มองเห็นได้ออกมา และหากเราเอาไปแยกว่ามีสีอะไรบ้าง (ดูสเปกตรัมของแสง) อาจจะด้วยปริซึมหรือเกรตติง เราจะพบว่าสีที่เปล่งออกมามีเพียงบางสีไม่ได้เป็นป้านของสีเหมือนกับที่เราเห็นในสายรุ้ง
หนึ่งคำอธิบายของสีที่ขาดช่วงมาจาก จอห์น วิลเลียม นิโคลสัน (John William Nicolson) ที่สนใจศึกษาดาราศาสตร์ผ่านสเปกตรัมของดวงดาว เขาเสนอว่าอิเล็กตรอนในอะตอมนั้นเรียงล้อมนิวเคลียสกันอยู่ในลักษณะที่เป็นวงแหวนกับลูกปัด ส่วนเส้นสเปกตรัมที่เราเห็นก็ออกมาจากการสั่นในสายธารของอิเล็กตรอน เขาใช้กลศาสตร์และทฤษฎีแม่เหล็กไฟฟ้าคลาสสิกในการทำนายค่าความยาวคลื่นที่ปรากฎออกมา14 งานของนิวโคลสันสำคัญเป็นอย่างยิ่ง ก็เพราะเหตุที่ว่าเขาก็เป็นคนแรกที่เชื่อมโยงค่าคงที่ของพลังค์เข้ามาในแบบจำลองอะตอม โดยเขาเสนอว่าอะตอมนั้นสามารถที่จะเสียหรือได้รับโมเมนตัมเชิงมุมได้ในเฉพาะบางค่าเท่านั้น นอกไปจากนั้น งานที่เขาทำก็ทำให้โปร์เข้าใจว่าการศึกษาสเปกตรัมนั้นเกี่ยวข้องกับโครงสร้างของอะตอมอย่างไร11
ก่อนไอเดียเรื่องโครงสร้างอะตอมของโปร์ที่ถูกเสนอ หนึ่งในคำบรรยายของสีของเส้นสเปกตรัมก็คือคำบรรยายผ่านสูตรของบาล์เมอร์ (Balmer’s formula) 15 บาล์มเมอร์เป็นนักดาราศาสตร์เขาเสนอสูตรนี้มาเพราะว่าเราจะเห็นเส้นสเปกตรัมในสูตรของเขาได้จากการส่องมองดวงดาวต่าง ๆ แม้ว่าดวงดาวทั้งหลายจะห่างกันหลายปีแสง หรือมีลักษณะที่แตกต่างกัน แต่เขาก็มักจะเห็นสเปกตรัมพวกนี้ได้จากดวงดาวต่าง ๆ ที่เป็นเช่นนี้ก็เพราะว่าสูตรของบาล์เมอร์นี้บรรยายความยาวคลื่นที่ถูกปล่อยออกมาจากการเย็นตัวลงของไฮโดรเจน อันเป็นส่วนประกอบสำคัญในดาวฤกษ์หลาย ๆ ดวง เพื่อที่จะเห็นภาพชัด ๆ เราขอเขียนสูตรของบาล์มเมอร์ออกมาว่า
เมื่อ
- λ คือความยาวคลื่น
- B ค่าคงที่ มีค่าประมาณ เมตร
- m คือจำนวนเต็ม
- n คือจำนวนเต็มที่น้อยกว่า m
นีลส์ โปร์ในปี 1913 หลังจากขบคิดเรื่องอะตอมมานาน (เขาชอบเจเจทอมสันเป็นการส่วนตัวและได้ติดต่อกับรัทเทอร์ฟอร์ดหลายครั้ง) เขาไปได้ยินเรื่องสูตรเส้นสเปกตรัมของบาล์เมอร์มาจากเพื่อนของเขาที่ศึกษาเรื่องสเปกตรัมที่ชื่อ ฮันส์ มาเรียส ฮันเซน (Hans Marius Hansen) 16 เขาก็ปิิ้งไอเดีย และตีความว่าสูตรนี้สะท้อนให้เห็นโครงสร้างของอะตอมที่มีลักษณะเป็นชั้น ๆ และมีเลขชั้นกำกับที่เป็นจำนวนเต็มชัดเจน11 เขาก็เสนอแบบจำลองเชิงควอนตัมของโครงสร้างอะตอม ที่อธิบายว่าอิเล็กตรอนในอะตอมมีวงโคจรบางวงโคจรที่เสถียร เมื่ออะตอมดูดกลืนหรือปลดปล่อยพลังงานผ่านคลื่นแม่เหล็กไฟฟ้า อิเล็กตรอนจะกระโดดจากวงโคจรหนึ่งไปสู่อีกวงโคจรหนึ่งในทันที พร้อมกับปลดปล่อยคลื่นแม่เหล็กไฟฟ้าที่มีค่าพลังงานเฉพาะ ซึ่งค่าจำเพาะนี้จะเป็นค่าที่ไม่ต่อเนื่อง และสัมพันธ์กับค่าความยาวคลื่นอย่างที่พลังค์ได้เสนอ 17
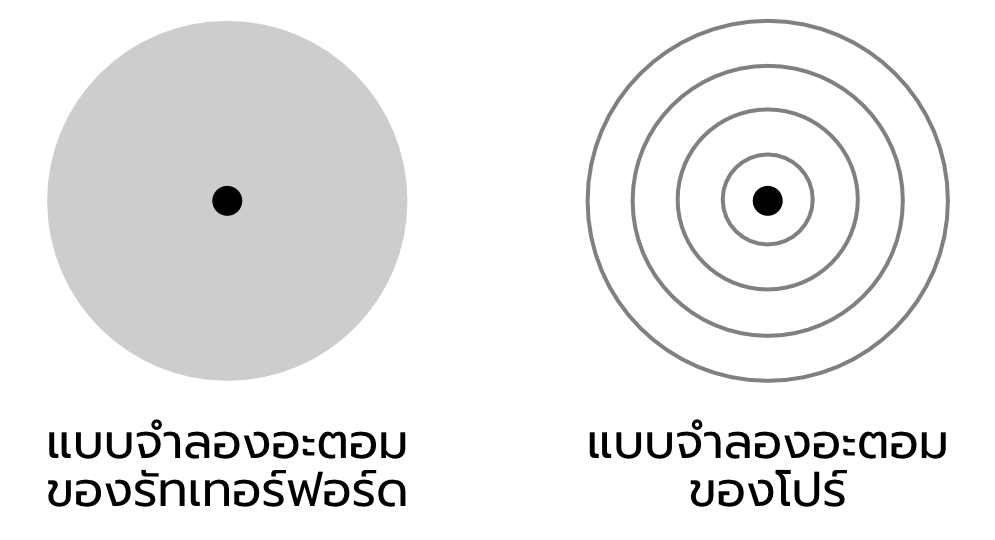 ภาพเปรียบเทียบแบบจำลองอะตอมของรัทเทอร์ฟอร์ดกับของโปร์ อิเล็กตรอนของในแบบจำลองของรัทเทอร์ฟอร์ดอยู่รอบนอกกินพื้นที่ส่วนใหญ่ของอะตอม ไม่ได้เจาะจงว่าจะอยู่ที่ใดที่หนึ่งเป็นพิเศษ ในขณะที่ของโปร์ระบุเจาะจงไปว่าอิเล็กตรอนจะอยู่ในวงโคจรเฉพาะเท่านั้น
ภาพเปรียบเทียบแบบจำลองอะตอมของรัทเทอร์ฟอร์ดกับของโปร์ อิเล็กตรอนของในแบบจำลองของรัทเทอร์ฟอร์ดอยู่รอบนอกกินพื้นที่ส่วนใหญ่ของอะตอม ไม่ได้เจาะจงว่าจะอยู่ที่ใดที่หนึ่งเป็นพิเศษ ในขณะที่ของโปร์ระบุเจาะจงไปว่าอิเล็กตรอนจะอยู่ในวงโคจรเฉพาะเท่านั้น
ทฤษฎีของโปร์อธิบายค่าสเปกตรัมที่มีค่าเฉพาะบางค่า ยืนยันว่าอิเลกตรอนในอะตอมนั้นไม่ปลดปล่อยหรือดูดกลืนพลังงานอย่างต่อเนื่อง อย่างที่คิด ๆ กันผ่านกลศาสตร์คลาสสิกและทฤษฎีแม่เหล็กไฟฟ้าของแมกซ์แวล เป็นการปฏิเสธกฏของฟิสิกส์คลาสสิกในระดับพื้นฐาน และยอมรับว่าเราต้องหาคำอธิบายในรูปแบบที่เป็นควอมตัมมาอธิบายเรื่องนี้ คำอธิบายแบบควอนตัมนี้เชื่อมโยงสเปกตรัมที่สังเกตได้จากดาวฤกษ์ โครงสร้างอะตอม และก็ค่าคงที่ของพลังค์เข้าด้วยกัน นอกจากนั้นยังอธิบายเรื่องการมีค่าควอนไทซ์ของโมเมนตัมเชิงมุมของอิเล็กตรอน ทว่าแบบจำลองนี้เพียงยืนยันว่าอิเล็กตรอนในอะตอมอยู่ได้อย่างเสถียรด้วยระดับชั้นพลังงานพิเศษ แต่ก็ไม่ได้อธิบายว่าเหตุใดจึงเป็นเช่นนั้น จนกระทั่งลูกท่านหลานเธอชาวฝรั่งเศษแห่งบ้านบรอยได้เข้ามาตอบเรื่องนี้
ความเป็นคลื่นของอนุภาค
หลุยส์ เดอบรอย (Louis de Broglie) ในวัย 32 ปีได้เสนอบางสิ่งเข้ามาในงานวิทยานิพนธ์ระดับปริญญาเอกของเขา เขาเสนอว่าสสารทุกอย่าง รวมถึงอิเล็กตรอนด้วย มีสมบัติของความเป็นคลื่นอยู่ เขาเสนอว่าค่าความยาวคลื่นของสสารเป็นไปตามสมการ
นั่นคือค่าความยาวคลื่นของสะสารมีค่าเท่ากับส่วนกลับของจำนวนเท่าของโมเมนตัมต่อค่าคงที่ของพลังค์18
สมมติฐานของเดอบรอยจะนำไปสู่การอธิบายว่าทำไมอิเล็กตรอนถึงมีวงโคจรที่สเถียรและเป็นจำนวนเท่าของค่าบางค่าเท่านั้น ไม่ได้เป็นค่าที่ต่อเนื่องกันไป ชายบ้านบรอยคนนี้ได้รับแนวคิดเรื่องการพิจารณาสมบัติความเป็นคลื่นของสสารมาจากระบบการคิดเกี่ยวกับกลศาสตร์ของฮามิลตันที่มีลักษณะคล้ายคลึงกันกับการเคลื่อนที่ของแสงที่จะเคลื่อนที่ผ่านเส้นทางที่เวลาสั้นที่สุด และก็ยังส่งผลให้ชโรดิงเจอร์พยายามจะค้นหาสมการคลื่นที่อธิบายพฤติกรรมของเจ้าคลื่นสสารนี้ จนทำให้เรามีสมการที่เรียกว่าสมการคลื่นของชโรดิงเจอร์ทีเป็นเหมือนกับรากฐานที่ใครเรียนฟิสิกส์ระดับมหาวิทยาลัยก็ต้องเจอ
ควอนไทเซชั่น: ธรรมชาติของโลกควอนตัม
ควอนไทเซชั่นคือหลักการบางอย่างที่ทำให้พลังงานหรือปริมาณอื่นในฟิสิกส์สามารที่จะรับหรือส่งได้เป็นค่าจำเพาะเท่านั้น คำอธิบายนี้เข้ามาแก้ปัญหาที่เกี่ยวข้องกับอิเล็กตรอนและอะตอม ผลการทำนายการวัดที่ออกมาผ่านปรากฎการณ์ต่าง ๆ ก็เที่ยงตรงมากขึ้น แต่ในธรรมชาติและตามความเป็นจริง อิเล็กตรอนจะรับพลังงานและส่งผ่านพลังงานในหน่วยที่เป็นก้อน ๆ จริง ๆ หรือเปล่า หรือการรับส่งแสง/คลื่นแม่เหล็กไฟฟ้าเท่านั้นที่มีลักษณะเป็นก้อน ที่อาจจะเป็นแบบอย่างหลังก็เพราะจะเห็นได้ว่าการทดลองก่อนหน้าทั้งหมดมีแสงหรือคลื่นแม่เหล็กไฟฟ้าเข้ามาเกี่ยวข้องทั้งสิ้น
ปัญหาที่ว่านี่เป็นที่ถกเถียงกันอยู่นาน จนกระทั่งมีการทดลองที่แสดงให้เห็นได้ว่า ควอนไทเซชั่นเหล่านั้นเป็นสิ่งที่เกิดขึ้นจริงในระดับชั้นพลังงานของอะตอม ไม่ใช่เพียงทริคของแสง หรือไม่ใช่เพียงทริคในการคำนวณเท่านั้น
การทดลองแรกที่แสดงให้เห็นว่าอะตอมนั้นรับพลังงานในค่าที่ไม่ต่อเนื่องจริง ๆ ก็คือการทดลองของแฟรงก์และเฮิร์ตซ์ (Franck–Hertz Experiment) ในปี 191419
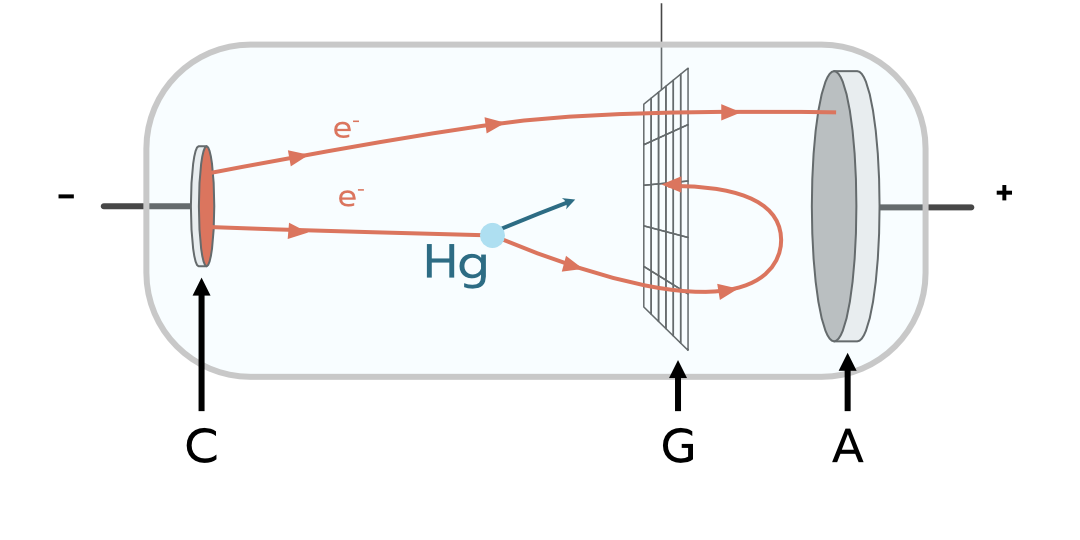 ภาพการทดลองของแฟรค์-เฮริตซ์ เส้นสีแดงแสดงเส้นทางการเคลื่อนที่ของอิเล็กตรอนสองตัว ตัวแรกวิ่งผ่านอย่างอิสระไปยังขั้วบวก ในขณะที่อิเล็กตรอนอีกตัววิ่งไปชนแบบไม่ยืดหยุ่นกับอะตอมของปรอท (แทนด้วยวงกลมสีฟ้า) ทำให้ศูนย์เสียพลังงานและไม่เหลือพลังงานพอที่จะไปต่อยังขั้วบวก
ภาพการทดลองของแฟรค์-เฮริตซ์ เส้นสีแดงแสดงเส้นทางการเคลื่อนที่ของอิเล็กตรอนสองตัว ตัวแรกวิ่งผ่านอย่างอิสระไปยังขั้วบวก ในขณะที่อิเล็กตรอนอีกตัววิ่งไปชนแบบไม่ยืดหยุ่นกับอะตอมของปรอท (แทนด้วยวงกลมสีฟ้า) ทำให้ศูนย์เสียพลังงานและไม่เหลือพลังงานพอที่จะไปต่อยังขั้วบวก
การทดลองนี้ใช้หลอดสุญญากาศที่ภายในบรรจุเฉพาะก๊าซของปรอท และมีแผ่นตัวนำขั้วบวกและลบอยู่ที่ปลายทั้งสองข้าง (C,A)เมื่อค่าความต่างศักย์ระหว่างสองปลายนี้สูงพอ ก็จะทำให้เกิดกระแสไฟฟ้าขึ้นระหว่างขั้วบวกและขั้วลบ พวกเขาวัดค่ากระแสที่เกิดขึ้นในวงจรนี้เมื่อเปลี่ยนค่าความต่างศักย์ระหว่างปลายทั้งสองด้านของแผ่นตัวนำ ทีนี้ เพื่อที่จะวัดว่าอิเล็กตรอนมีพลังงานเท่าไหร่ เอาตาข่ายตัวนำ (G) มาวางไว้เบื้องหน้าของแผ่นตัวนำขั้วบวก โดยแผ่นตัวนำนี้จะมีความต่างศักย์ระหว่างขั้วลบกับตัวมันที่มากกว่าระหว่างขั้วบวกกับขั้วลบ ทำให้อิเล็กตรอนบางตัวที่เข้าไปชนกับอะตอมและเสียพลังงานให้อะตอม ไม่มีพลังงานมากพอที่จะไปต่อยังขั้วบวก
 ภาพสร้างใหม่จากผลการทดลองต้นฉบับของแฟรงก์และเฮิร์ตซ์ ภาพจากวิกิมีเดีย
ภาพสร้างใหม่จากผลการทดลองต้นฉบับของแฟรงก์และเฮิร์ตซ์ ภาพจากวิกิมีเดีย
ผลการทดลองพบว่ากระแสไฟฟ้านั้นตกลงกระทันหันในบางค่าความต่างศักย์ ซึ่งแสดงให้เห็นว่าอะตอมรับพลังงานได้ในค่าเฉพาะบางค่าเท่านั้น เนื่องจากการทดลองนี้ไม่มีการวัดที่เกี่ยวกับแสงมาเกี่ยวข้องเลย ทำให้เราเห็นว่าธรรมชาติของอะตอมเป็นแบบที่โปร์เสนอจริง ๆ
ไม่เพียงแต่ค่าพลังงานของอิเล็กตรอนในอะตอมเท่านั้นที่มีค่าไม่ต่อเนื่อง ค่าทางฟิสิกส์อื่น ๆ ก็สามารถแสดงสมบัติว่ามันมีค่าได้เพียงบางค่าเช่นเดียวกัน หนึ่งในนั้นก็คือค่าโมเมนต์แม่เหล็กและรวมถึงทิศทางของมัน สมบัตินี้ปรากฏตัวให้เราเห็นครั้งแรกแผ่านการทดลองของ สเติร์น–เกอร์ลาค (Stern-Gerlach experiment) 20
 By Tatoute - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=34095239
By Tatoute - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=34095239
การทดลองนี้ยิงอะตอมเงินผ่านสนามแม่เหล็ก อะตอมที่มีโมเมนต์แม่เหล็กอย่างอะตอมของเงินก็จะถูกทำให้โค้ง จะโค้งมากหรือน้อยก็ขึ้นกับว่าทิศทางของโมเมนต์แม่เหล็กของอะตอมกับทิศทางของสนามทำมุมกันมากเท่าใด ซึ่งถ้ายิงออกไปสุ่ม ๆ ผลที่ควรจะได้คือเลข 4 อะตอมตกลงบนฉากปรากฏเป็นเส้นซึ่งเป็นผลที่ฟิสิกส์ในยุคก่อนหน้านั้นทำนาย แต่ว่าผลการทดลองเป็นไปตามเลข 5 ในภาพซึ่งเป็นผลที่แสดงให้เห็นว่าทิศของโมเมนต์แม่เหล็กของอะตอม (สปิน) มีธรรมชาติที่เป็นแบบควอนตัม คือเป็นได้เฉพาะบางค่า ในที่นี้คือได้เพียงแค่สองค่าเท่านั้น
การทดลองทั้งสองนี้ตอกย้ำว่าควอนไทเซชั่นไม่ได้เพียงช่วยให้เราคำนวณค่าอื่น ๆ ในปลายทางอย่างถูกต้อง หรือปรากฏตัวแค่ในกรณีที่มีอิเล็กตรอนหรือแสง แต่เป็นสิ่งที่ธรรมชาติเป็นจริง ๆ แต่ยิ่งไปกว่านั้น ใช่ว่าปรากฎการณ์ควอนตัมจะเผยออกมาในระดับเล็ก ๆ เท่านั้น ในระบบที่ใหญ่แต่หากมีการควบคุมและลดสัญญาณรบกวนจากภายนอกที่ดีเพียงพอก็สามารถแสดงพฤติกรรมแบบควอนตัมได้เช่นกัน
สรุป
การทดลองและผลการทดลองทั้งหมดที่กล่าวมาเป็นสิ่งที่ทำให้เราไม่สามารถปฏิเสธได้ว่าธรรมชาติไม่ได้ประพฤติตัวตามทฤษฎีคลาสสิกที่เรามีมา แต่ประพฤติตัวตามทฤษฎีที่มีกฎและหลักการบางอย่างที่ทำให้พลังงานที่รับ/ส่งได้เป็นค่าจำเพาะเท่านั้น ความไม่ต่อเนื่องของค่าทางฟิสิกส์เหล่านี้เป็นหนึ่งในคุณลักษณะสำคัญที่นำไปสู่ทฤษฎีควอนตัมยุคเก่า (The old quantum theory) และภายหลังก็กลายเป็นกลศาสตร์ควอนตัม อันเป็นรากฐานของทฤษฎีควอมตัมทั้งหลาย ในบทความต่อ ๆ ไปเราจะไปสำหรวจกันว่าในกลศาสตร์ควอนตัม มีคุณลักษณะอื่น ๆ ใดอีกบ้างที่โดดเด่นหรือแตกต่างไปจากทฤษฎีคลาสสิกที่เรามี
อ้างอิงและข้อมูลเพิ่มเติม
Footnotes
-
W. Wien, “XXX. On the division of energy in the emission-spectrum of a black body,” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, vol. 43, no. 262, pp. 214–220, Mar. 1897, doi: 10.1080/14786449708620983. ↩
-
M. Planck, “Ueber das Gesetz der Energieverteilung im Normalspectrum,” Annalen der Physik, vol. 309, no. 3, pp. 553–563, Jan. 1901, doi: 10.1002/andp.19013090310. English Translation available at https://strangepaths.com/files/planck1901.pdf. ↩
-
ʻabd Al-Ḥamīd Ṣabra, Theories of light from Descartes to Newton. Cambridge: Cambridge University Press, 1981. ↩
-
I. Newton, “A letter of Mr. Isaac Newton, Professor of the Mathematicks in the University of Cambridge; containing his new theory about light and colors: sent by the author to the publisher from Cambridge, Febr. 6. 1671/72; in order to be communicated to the R. Society,” Phil. Trans. R. Soc., vol. 6, no. 80, pp. 3075–3087, Feb. 1672, doi: 10.1098/rstl.1671.0072. ↩
-
I. Newton, Opticks: Or, A Treatise of the Reflections, Refractions, Inflections, and Colours of Light. New York: Dover Publications, 1952. Also accessible online at: https://www.gutenberg.org/cache/epub/33504/pg33504-images.html. ↩
-
C. C. Silva and B. A. Moura, “Science and Society: The Case of Acceptance of Newtonian Optics in the Eighteenth Century,” Sci & Educ, vol. 21, no. 9, pp. 1317–1335, Sept. 2011, doi: 10.1007/s11191-011-9380-1. ↩
-
“VIII. A dynamical theory of the electromagnetic field,” Phil. Trans. R. Soc., vol. 155, pp. 459–512, Dec. 1865, doi: 10.1098/rstl.1865.0008. ↩
-
M. Fowler, “Photoelectric Effect,” galileo.phys.virginia.edu., Accessed: Oct 10, 2025, [Online], Available: https://galileo.phys.virginia.edu/classes/252/photoelectric_effect.html ↩
-
J.J. Thomson, "On Bodies Smaller Than Atoms", Popular Science Monthly, Vol.59 (1901), Access: https://en.wikisource.org/wiki/Popular_Science_Monthly/Volume_59/August_1901/On_Bodies_Smaller_Than_Atoms. ↩
-
P. Lenard, “Erzeugung von Kathodenstrahlen durch ultraviolettes Licht,” Annalen der Physik, vol. 307, no. 6, pp. 359–375, Jan. 1900, doi: 10.1002/andp.19003070611. ↩
-
M. Jammer, The conceptual development of quantum mechanics, Tomash Publishers, American Institute of Physics, 1989. Also available online: https://archive.org/details/max-jammer.-the-conceptual-development-of-quantum-mechanics/. ↩ ↩2 ↩3
-
A. Einstein, “Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt,” Annalen der Physik, vol. 322, no. 6, pp. 132–148, Jan. 1905, doi: 10.1002/andp.19053220607. English Translation from Wikisource ↩
-
G. Holton, Quantum Milestones, 1916: Millikan’s Measurement of Planck’s Constant, "American Physics Society", Physics, [Online], Accessed: Oct 22, 2025, Available: https://physics.aps.org/articles/v18/12 ↩
-
J. W. Nicholson, “The Spectrum of Nebulium,” Monthly Notices of the Royal Astronomical Society, vol. 72, no. 1, pp. 49–64, Nov. 1911, doi: 10.1093/mnras/72.1.49. ↩
-
“ChemTeam: The Balmer Formula,” Chemteam.info, 2024. https://www.chemteam.info/Electrons/Balmer-Formula.html ↩
-
N. Bohr, “I. On the constitution of atoms and molecules,” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, vol. 26, no. 151, pp. 1–25, July 1913, doi: 10.1080/14786441308634955. ↩
-
L. de Broglie, “Recherches sur la théorie des quanta,” Thesis, University of Paris, 1924. English Translation ↩
-
อ่านรายละเอียดการทดลองต่อได้ที่ UCSB Physics Remote Labs, "The Franck-Hertz Experiment", https://ilg.physics.ucsb.edu/Courses/RemoteLabs/index.html?linkfile=FH_Remote ↩
-
W. Gerlach and O. Stern, “Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld,” Z. Physik, vol. 9, no. 1, pp. 349–352, Dec. 1922, doi: 10.1007/bf01326983. ↩
-
M. Pihl, “H.M. Hansen,” Dansk Biografisk Leksikon | Lex, Jul. 17, 2011. https://biografiskleksikon.lex.dk/H.M._Hansen (accessed Oct. 18, 2025). ↩